ARCHS4：大规模转录组预处理数据库

2025-03-26

公开的转录组数据集多为原始形式，格式不统一、处理方式各异，难以有效利用，所以我想找一个经过标准流程清洗了GEO/SRA数据集的数据库，这样可以直接用清洗后的结果，而不用每个数据集单独处理。recount2（https://jhubiostatistics.shinyapps.io/recount/）就是类似的数据库，但只提供了2038个数据集，远远不够。

今天发现了ARCHS4（https://archs4.org/），感觉满足我目前的需求。ARCHS4数据源于GEO 和 SRA 数据库，还纳入了线虫、果蝇等其他物种的 35000 个样本数据，用的比对软件是Kallisto。数据维护一直在更新，还提供了分析和下载工具（https://github.com/MaayanLab/archs4py）。

RNA-Seq这块，提供了966693个样本比对结果，还提供了样本的tSNE结果，基因相关性结果。

2D color gradient

2025-02-15

Default Category

对于热图大家都熟悉，热图中的颜色表示值的大小。但前几天看到一个热图，里面的颜色含有两个维度的信息，专门有一个颜色的图注（非主图，而是热图里面的颜色说明），如下，横坐标表示D值的大小，纵坐标表示的P值，可以看出二维区域中不同位置的颜色，同时反应了D值和P值的信息。

找了很多工具和方法，都不太方便实现，或者不太容易控制颜色的分布。后来突然悟了，我可以自己生成这个图，从左到右反应的D值大小，两个颜色渐变，从上往下反应的是P值显著性，颜色越来越深。

Sequencing methods

2024-04-22

Default Category

Chip-Seq

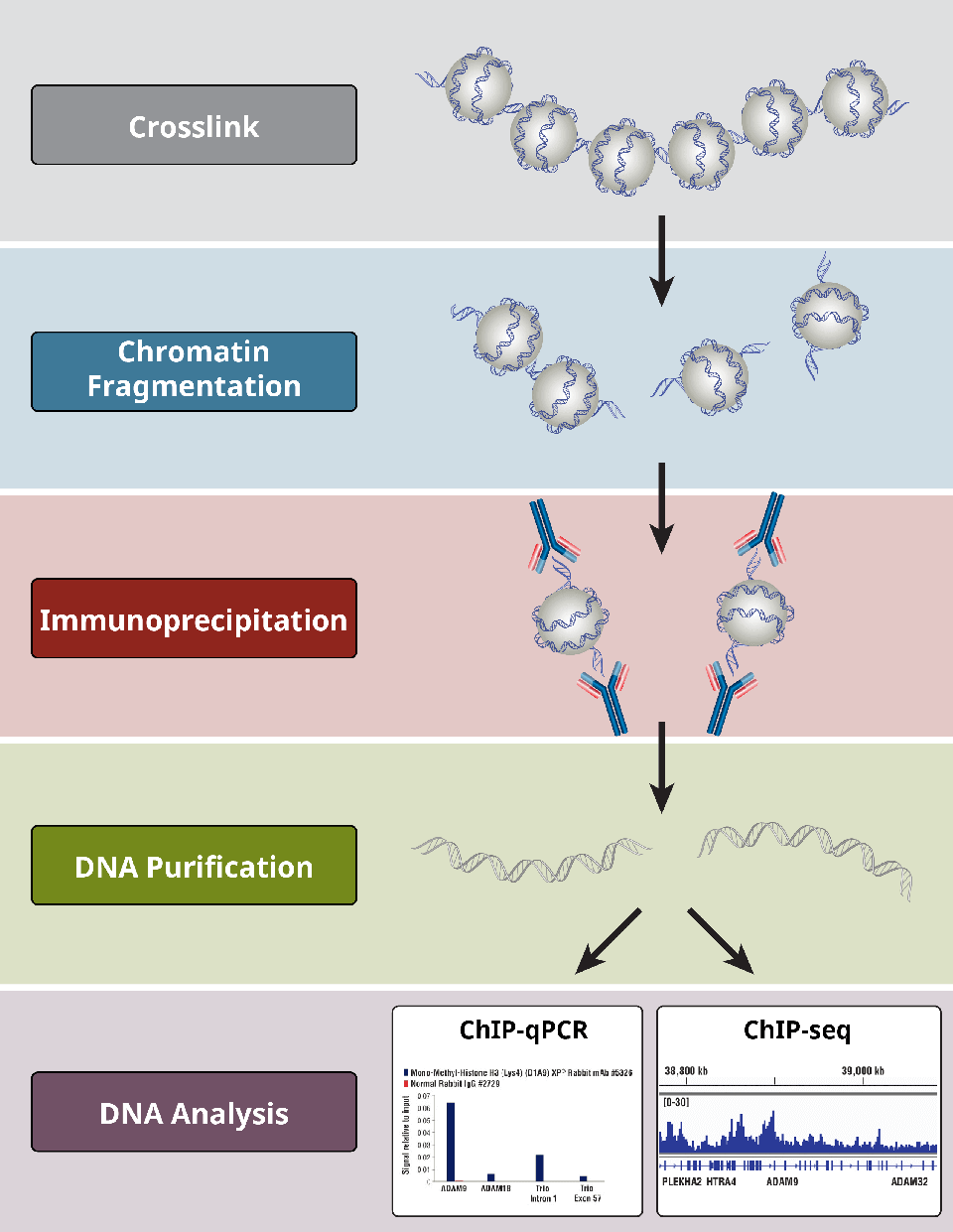
染色质免疫共沉淀（Chromatin Immunoprecipitation，ChIP）与二代测序相结合的表观遗传研究技术，能够高效地在全基因组范围内对DNA和蛋白的相互作用进行检测，通常用于转录因子结合位点或组蛋白特异性修饰位点的研究。

染色质免疫沉淀法 (ChIP) 是一种基于抗体的技术，可用来选择性地使特异性 DNA 结合蛋白及其 DNA 靶标富集。ChIP 可用来研究某种特殊的蛋白-DNA 相互作用、多种蛋白-DNA 相互作用或全基因组或部分基因内的相互作用。

ChIP 使用可选择性地检测和结合蛋白的抗体，包括组蛋白、组蛋白修饰、转录因子、辅因子，以提供有关染色质状态和基因转录的信息。在 ChIP 中结合使用蛋白质组分析和分子生物学技术，能够让研究者理解目的细胞或组织中的基因表达和调节。

Hi-C

Hi-C技术源于染色体构象捕获（Chromosome Conformation Capture, 3C）技术，利用高通量测序技术，结合生物信息分析方法，研究全基因组范围内整个染色质DNA在空间位置上的关系，获得高分辨率的染色质三维结构信息。Hi-C技术不仅可以研究染色体片段之间的相互作用，建立基因组折叠模型，还可以应用于基因组组装、单体型图谱构建、辅助宏基因组组装等，并可以与RNA-Seq、ChIP-Seq等数据进行联合分析，从基因调控网络和表观遗传网络来阐述生物体性状形成的相关机制。

PROGENy pathway signatures

2024-02-05

Default Category

PROGENy is resource that leverages a large compendium of publicly available signaling perturbation experiments to yield a common core of pathway responsive genes. For each pathway, a collection of genes are available along their contribution and significance to it. Inside PROGENy, one can find gene signatures for 14 different pathways: Androgen: involved in the growth and development of the male reproductive organs. EGFR: regulates growth, survival, migration, apoptosis, proliferation, and differentiation in mammalian cells Estrogen: promotes the growth and development of the female reproductive organs.

SAM/BAM文件中的MD标签

2024-01-29

Default Category

我用bowtie比对了序列，想查看reads的错配情况。SAM flag中的M包含了比对上的碱基和错位的碱基，不能区分错配。

参考bowtie的文档，可以看到XM的标签可以指示mismatch的个数，MD标签可以查看具体的错配情况。


`XN:i:<N>`	The number of ambiguous bases in the reference covering this alignment. Only present if SAM record is for an aligned read.
`XM:i:<N>`	The number of mismatches in the alignment. Only present if SAM record is for an aligned read.
`MD:Z:<S>`	A string representation of the mismatched reference bases in the alignment. See SAM Tags format specification for details. Only present if SAM record is for an aligned read.

SAM手册对与MD的介绍

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


String encoding mismatched and deleted reference bases, used in conjunction with the CIGAR and SEQ fields to reconstruct the bases of the reference sequence interval to which the alignment has been mapped. This can enable variant calling without requiring access to the entire original reference.
编码错配或del的字符串，与CIGAR和SEQ一起使用，重建read的比对情况。可以在不需要整个参考序列的情况下，用于突变检测。

The MD string consists of the following items, concatenated without additional delimiter characters:
MD字符串由以下不含分隔符的条目组成。

• [0-9]+, indicating a run of reference bases that are identical to the corresponding SEQ bases;表示与相应SEQ碱基相同的一系列参考碱基；这里[0-9]+是正则表示。
• [A-Z], identifying a single reference base that differs from the SEQ base aligned at that position;在这个位置SEQ碱基与参考碱基不一致
• \^[A-Z]+, identifying a run of reference bases that have been deleted in the alignment.以^开头，表明有个del，注意del前有^。

总结：数字表示匹配，碱基表示错配，^碱基表示del。

As shown in the complete regular expression above, numbers alternate with the other items. Thus if two mismatches or deletions are adjacent without a run of identical bases between them, a ‘0’ (indicating a 0-length run) must be used to separate them in the MD string. 数字和字符交替出现，如果两个连续错配，中间需要用0来隔开。

Clipping, padding, reference skips, and insertions (‘H’, ‘S’, ‘P’, ‘N’, and ‘I’ CIGAR operations) are not represented in the MD string. When reconstructing the reference sequence, inserted and soft-clipped SEQ bases are omitted as determined by tracking ‘I’ and ‘S’ operations in the CIGAR string. (If the CIGAR string contains ‘N’ operations, then the corresponding skipped parts of the reference sequence cannot be reconstructed.)
Clipping, padding, reference skips, and insertions (‘H’, ‘S’, ‘P’, ‘N’, and ‘I’ CIGAR operations)不体现在MD字符串中，所以要与CIGAR结合。

For example, a string ‘10A5^AC6’ means from the leftmost reference base in the alignment, there are 10 matches followed by an A on the reference which is different from the aligned read base; the next 5 reference bases are matches followed by a 2bp deletion from the reference; the deleted sequence is AC; the last 6 bases are matches.
10A5^AC6表示10个匹配（10），一个与A不匹配（A），2bp的del（^AC），6碱基的匹配。