临床模型的决策曲线分析解读
文章目录
朋友问如何解读决策曲线分析,正好我也顺便学习一下,看到这篇文章[A simple, step-by-step guide to interpreting decision curve analysis](A simple, step-by-step guide to interpreting decision curve analysis),这篇文章引用也100多了。
[TOC]

Abstract
背景
决策曲线分析是一种评估预测模型和诊断测试的方法,该方法在 2006 年的出版物中引入。 现在文献中普遍报道了决策曲线,但对其含义的理解仍然存在广泛的误解和混淆。
评论总结
在本文中,我们一步一步的解读决策曲线分析,并回答了有关该方法的一些常见问题。 我们认为,解释决策曲线的许多困难可以通过将 y 轴重新标记为“收益”并将 x 轴重新标记为“偏好”来解决。 如果模型或测试在一系列临床合理偏好中具有最高水平的益处,则可以推荐用于临床使用。
结论
如果读者和作者遵循一些简单的指导方针,决策曲线很容易理解。
引言
决策曲线分析是一种评估预测模型和诊断测试的方法,由 Vickers 和 Elkin 在 2006 年的 Medical Decision Making刊物上提出。该方法试图克服传统统计指标的局限性,例如区分和校准,因为它们不能直接提供临床价值信息以及完整决策分析方法,这些方法不适用于常规生物统计学实践。
简而言之,与治疗所有患者或不治疗患者的默认策略相比,决策曲线分析计算一个或多个预测模型或诊断测试的临床“净收益(net benefit)”。净收益是基于一系列阈值概率(0-1)计算的。
阈值概率(threshold probability)定义为需要进一步干预的疾病的最小概率,我们可以理解为风险概率。
净收益(net benefit) = sensitivity × prevalence – (1 – specificity) × (1 – prevalence) × w (这个公式多了prevalence)
对于给出疾病预测概率 p̂ 的预测模型,在特定的pt阈值下,w是比值比odds,等于p̂/(1-p̂),阳性样本的 p̂ ≥ pt,进而可以计算灵敏度和特异性。净收益不同于判别和校准等准确度指标,因为它包含了基于模型或测试做出的决策的后果。有关决策曲线分析背景的更多信息,参阅 Vickers 等人。
06年文章中简单的公式没有prevalence,如下

近年来,决策曲线分析的实际应用出现了爆炸式增长。该论文被广泛引用,截至 2019 年 5 月在 Google Scholar 上被引用超过 1000 次。决策曲线分析已被许多顶级期刊的社论推荐,包括 JAMA、BMJ、Annals of Internal Medicine、Journal of Clinical Oncology 和 PLoS Medicine。
但是,大家对决策曲线分析似乎存在误解和混淆。例如,一位受人尊敬的流行病学家声称,他在世界上还没有找到几个人可以解释决策曲线的含义,而他本人也不清楚他们的解释。作者在会议中碰到过,演示者展示了决策曲线幻灯片,然后他们自己评论他们实际上并不理解它。
这篇文章介绍了详细解读决策曲线分析的步骤。每一步都旨在加深理解。掌握任一步至少对已发布的决策曲线有所了解。先前社论中,主要是分析人员报告决策曲线分析,与此相反,这篇文章的主要受众是希望了解已发布决策曲线的读者。在这篇文章中的场景是个别患者的情况,例如有小孩并担心癌症的患者。示例仅用于教学目的:因为决策曲线是一种研究工具,不能直接用于临床。还要注意的是这篇文章不评论如何计算决策曲线,也不会评论它们的数学特性。计算方法读者可以参考 www.decisioncurveanalysis.org (PS:这个网页下有基于Stata,R和SAS的代码,用于分析DCA),可以参考这篇文章的参考文献或者06年的文章。
文章中使用的示例是前列腺癌活检研究,这同时也不仅仅是一个示例,因为该研究在多篇决策曲线分析的研究中北多个机构用于比较两个模型。作为背景,接受前列腺特异性抗原 (PSA) 筛查的男性如果 PSA 升高(例如 3 ng/mL 或更高),通常建议进行活检。然而,这些男性中只有一小部分患有高级别癌症,这种癌症可以从早期治疗中受益。相比之下,低级别癌症则经常被过度诊断,当然,泌尿科医生不会建议对没有癌症的男性进行活检。研究人员试图寻找其他标志物来预测 PSA 升高的男性的高级别癌症。这个想法是,任何 PSA 升高的人都将接受第二次测试,并且只有在表明患侵袭性疾病的高风险时才会进行活检。在我们的假设研究中,高级别癌症的患病率(prevalence )为 10%。我们假设该研究评估了二元诊断测试(敏感性 40%,特异性 90%)和基于几个标志物的统计预测模型,这个模型的曲线下面积(AUC ) 为0.79。
解读决策曲线分析
步骤 1:收益好 Benefit is good
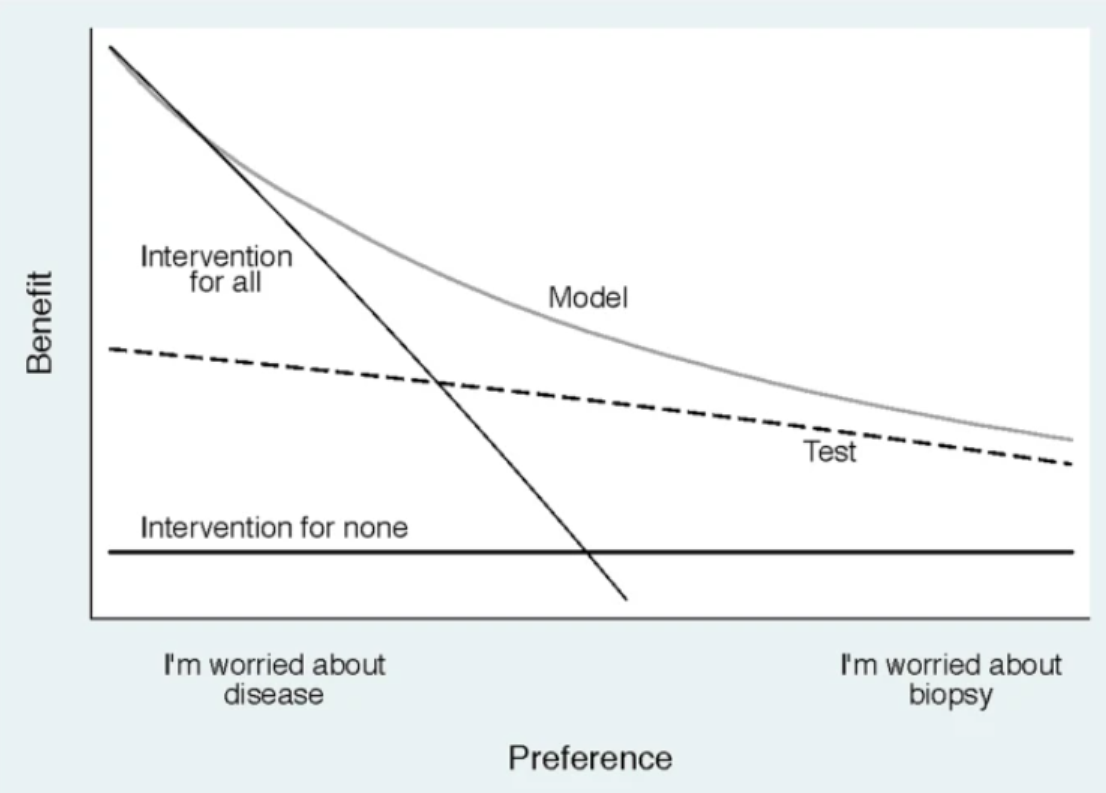
图 1收益与偏好的决策曲线
图 1 仅显示了决策曲线分析的最基本要素。预测模型的结果是浅灰色线,诊断测试是虚线。另外两条线是“干预所有人”(细黑线)和“不干预任何人”(粗黑线)。
“干预”(Intervention):它可能指药物或手术,但也可能包括生活方式建议、额外的诊断检查或后续监测。干预反映了模型中处于高风险的患者或在诊断测试中获得阳性结果的患者,在考虑改善他们的健康或他们的整体生活的任何行动。特定的干预取决于临床环境。在我们对 PSA 升高的男性前列腺癌的研究中,干预意味着前列腺活检。举其他例子,在感染研究中,干预可能是给予抗生素;在一项心脏病预防研究中,干预可能是给予他汀类药物。在一项晚期癌症姑息性手术的研究中,3个月内死亡;然而,这个想法是避免对高风险患者进行手术,干预将是“最好的支持性护理”。在描述决策曲线分析的原始论文中,以及在许多实证应用中,也有使用“治疗”一词来代替干预。
决策曲线分析包括“干预所有人”和“不干预任何人”的结果,因为这些也通常是合理的临床策略。举一个具体的例子,前列腺活检研究中的一种合理策略是对所有 PSA 升高的患者进行活检,而不管诊断测试或预测模型的结果如何。实际上,在真正的临床实践中也会发生的,比如 PSA 高于某个阈值的男性通常会在没有额外测试的情况下进行活检。另一方面,我们可以想象一项针对 PSA 低的男性的研究,这些男性在常规临床实践中无需进行活检。其中一些男性确实患有高级别前列腺癌,研究人员可能正在研究合适的测试(例如模型或者标志物)。在这种情况下,参考策略将是“不干预”。
在图中,y 轴是收益Net benefit,x 轴是偏好。测试或模型的好处是它可以正确识别哪些患者有病和没有病(在我们的例子中,是高级别癌症)。偏好是指医生如何评价给定患者的不同结果,通常受到医生和患者之间讨论也会影响该决定。下面将更详细地描述偏好和收益:在这个阶段,重要的是要知道收益是好的但偏好会有所不同。很容易看出,对应于预测模型的浅灰色线在广泛的偏好值范围内具有最高的收益。因此可以得出结论,除了小范围的低偏好外,基于预测模型对患者进行干预(即活检)比对所有患者活检、不活检或仅活检诊断测试呈阳性患者。对于前列腺活检研究,结论是使用该模型来确定患者是否应该进行活检会改善临床结果。
步骤2: 偏好是指医生如何评价患者的不同结果Preference refers to how doctors value different outcomes for their patients
在与一些患者进行咨询和讨论后,医生可能会特别担心漏诊;对于其他患者,医生可能更关心避免不必要的干预。医生的干预倾向也可能不同,有些更保守,有些更激进。在图 1 中,偏好的 x 轴的极端情况是“我担心疾病”和“我担心活检”。在前列腺癌活检的场景中,对于给定患者,偏向于 x 轴左端的医生认为错过高级别癌症的相对危害远大于不做活检的危害。例如,有的患者年龄很小且是学龄儿童,要优先考虑在可治愈阶段发现任何致命癌症:该患者显然“担心疾病”,符合继续治疗的低门槛诊断检查(也就是说倾向于活检)。另外一种情况,倾向于x轴右侧的医生希望患者尽量避免活检,这可能反映了患者不喜欢侵入性检测的想法,另外一种情况医生也倾向于尽量避免活检,比如对检测的价值持怀疑态度。通常他们只会在活检患者处于特别高的风险中才建议患者进行活检。
这有助于对决策曲线的进一步解读,我们可以看到,“非常担心”类别的医生外(倾向于对所有人进行干预),对于“全民干预”策略的收益略高于模型,除此之外的其他阈值范围内,模型比其他方法具有更高的收益。这具有直观的意义:PSA 升高的患者强烈倾向于早期识别潜在的致命癌症,他们可能希望直接进行活检,而不是依赖并非 100% 准确的第二个模型或测试。
步骤 3:偏好单位是阈值概率The unit of preference is threshold probability
我们的模型给出了患者患高级别癌症的预测概率。有人可能会假设,如果模型将患者的风险估计为 1%,那么患者和医生都会同意不需要进行活检;但是,如果风险为 99%,医生会建议并且患者接受活检的指征。如果风险分别为 2% 和 98%,将得出类似的结论。我们可能会想象我们会改变风险值,从 2% 向上计数,从 98% 向下计数,直到医生不再确定。例如,一位医生可能会说:“我不会用超过10次活检的概率来在健康状况相似的患者中发现一种高级别病变并且考虑活检的收益和风险。因此,如果患者的风险超过 10%,我会让患者进行活检,否则,我只会仔细监测患者,如果我发现有其他证据的话可能会在稍后进行活检。”
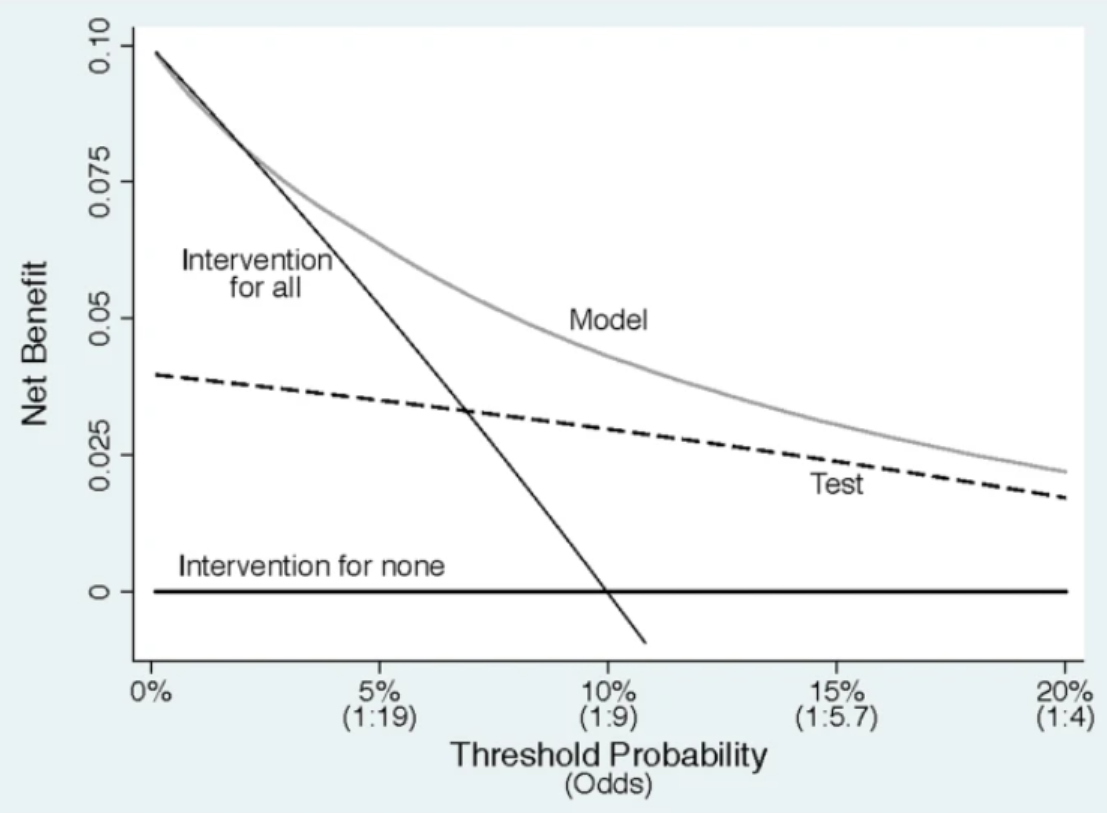
图2 DCA曲线中收益net benefit与阈值概率threshold probability
使用odds时,偏好和阈值概率之间的关系是最容易看到的。10% 的风险是 1:9 的几率,因此在使用 10% 的阈值概率时,医生告诉我们“错过高级别癌症比进行不必要的活检差 9 倍”。这可以解释为“需要测试的数量”,即 10% 是需要测试的数量 10。图 2 显示了 x 轴上的阈值概率。odds也出于教学目的而显示,尽管在呈现决策曲线时省略了这些。这有助于我们理解我们之前的结论,即特别担心疾病的患者不会从使用该模型中受益。我们现在可以看到,只有当阈值概率小于 2% 或 3% 时,我们才应该避免使用该模型。这将是前列腺癌的一个延伸,活检是侵入性的、痛苦的,并且与败血症的风险相关。然而,在其他一些情况下,如此低的阈值可能是合理的,例如皮肤癌活检,这是一种风险小得多且侵入性小得多的手术。另请注意,曲线仅绘制到 20%。这是因为,鉴于与活检的危害相比,漏诊高级别前列腺癌的相对风险,我们认为任何患者或医生在接受活检之前要求超过 20% 的风险是不合理的。因此,阈值的合理范围主要取决于上下文。在其他地方,我们详细描述了如何取得合理的阈值范围。
步骤4:
图 2 还显示了收益的单位,即所谓的“净收益”。 “净收益”中的“净”与“净利润”中的“净”相同,即收入减去支出。例如,如果葡萄酒进口商从法国购买 100 万欧元的葡萄酒并以 150 万美元的价格在美国出售,那么如果汇率为 1 欧元兑 1.25 美元,则净利润为美元收入(150 万美元)-欧元支出(1m) × 汇率 (1.25) = 250,000 美元。为了简单起见,撇开风险问题以及交易的时间和麻烦不谈,这相当于在无需进行任何交易的情况下获得了 250,000 美元。在诊断的情况下,收入是真阳性(例如,发现癌症),支出是假阳性(例如,不必要的活检),“汇率 ”是值得发现一个真阳性而允许的假阳性数量(odds?)。汇率将取决于干预(intervention)和结果(outcome)的相对严重性。例如,活检过程是安全的还是危险的,或者癌症是侵袭性的还是惰性的,我们是否进行更多不必要的活检来发现一种癌症。如上所述,汇率是根据阈值概率计算的。类似于净健康收益或净货币收益,它们都取决于在交换健康和成本方面的收益时支付门槛的意愿。
净收益的单位是真阳性。例如,0.07 的净收益意味着“目标人群中每 100 名患者中有 7 名真阳性”。因此,就像葡萄酒贸易商的净利润示例一样,0.07 的净收益相当于每 100 名患者中识别出 7 名患有疾病的患者。在前列腺活检示例中,0.07 的净收益相当于每 100 名患者进行活检,将发现有 7 名患者患有高级别肿瘤的策略。同样与商业示例相比,250,000 美元的利润可能来自各种收入和支出组合,0.07 的净收益可能来自真假阳性的不同组合。
步骤5:净收益也可以表示为被避免干预(干预减少)Net benefit can also be expressed as interventions avoided
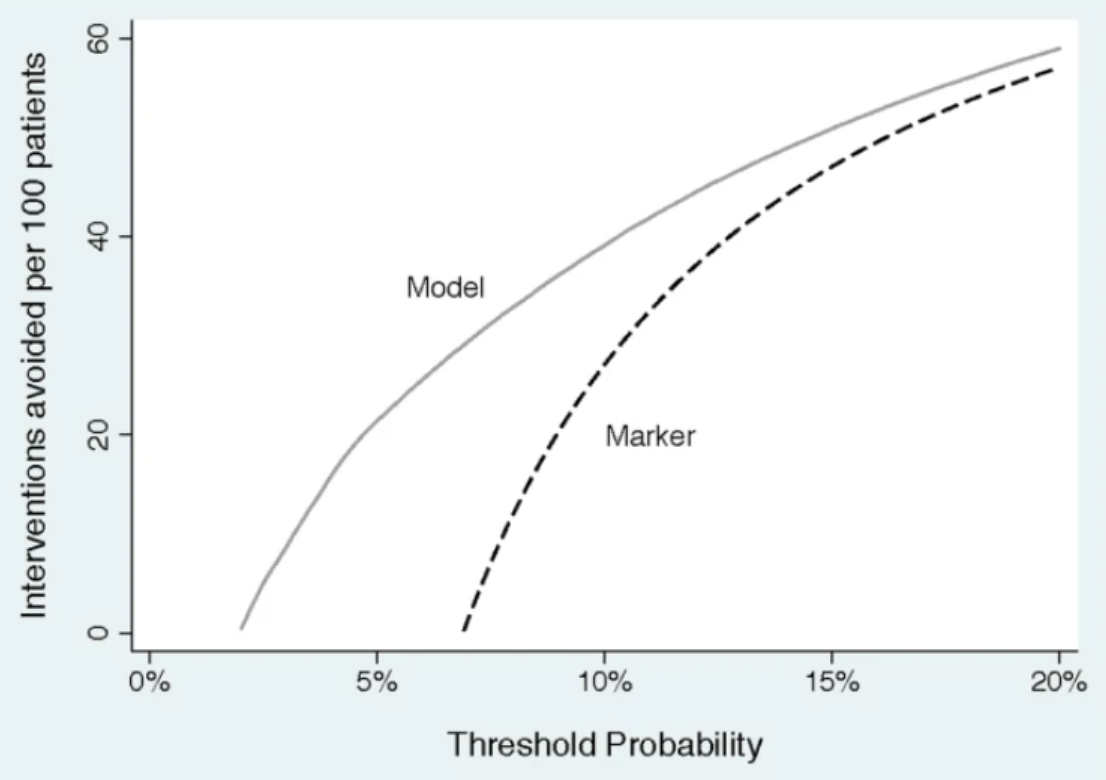
图3 A DCA曲线中干预 interventions 的减少 与阈值概率 threshold probability
在许多情况下,最常见的策略是“干预所有人”,而不是“不干预任何人”。事实上,我们的前列腺癌示例就是这种情况,泌尿科医生会定期对所有 PSA 升高的患者进行活检。在这些情况下,模型或测试旨在减少不必要的干预。净收益可以用真阴性而不是真阳性来表示。图 3 显示了此类决策曲线的示例。这可以解释为,在 10% 的风险阈值下,使用预测模型可以减少40%的活检数目,而不会错过任何高级别癌症患者的活检。如果与“干预所有人”想比较,就避免不必要的诊断程序或避免不必要的治疗方面,推荐用净收益来表达。请注意,这样做不会改变关于哪个模型或测试具有最高净收益的结论。
关于解读决策曲线的一些常见问题
如果我们不知道阈值概率怎么办?
使用任何模型或测试时,阈值概率都是非常重要的。如果前列腺癌预测模型给出的预测风险为 40%,并且没有人知道该风险是高还是低,因此无法判断是否需要活检,那么该模型就不能用于做出决定。因此,使用决策分析技术(例如决策曲线分析)不适用于评估该模型。
如何考虑治疗效果?
在大多数决策曲线中,治疗效果是隐含的,并被纳入阈值概率中。一般来说,治疗越有效,阈值概率越低。在前列腺癌的例子中,高级别疾病的诊断非常重要,因此如果诊断和治疗高级别癌症对预期寿命有更大的影响,概率阈值会更低。另一个简单的例子,考虑一个预测心脏病发作的决策曲线,其中给予高危患者预防性药物。想象一下,该药物将心脏事件的相对风险降低了10%,但会增加1%绝对中风或胃肠道出血等严重副作用的风险。如果我们假设心脏事件和严重副作用有相同的危害,那么证明治疗合理的最小阈值概率为 10%。因为从阈值概率10%这个特定值下降低10%的相对风险的值也是1%(10%*10%=1%),这时心脏事件风险的降低与中风风险的增加相同(如果在10%以上的阈值概率下,中风的风险增加比心脏事件降低的概率高)。但是,如果药物更有效,例如降低 20% 的相对风险,那么最小阈值概率将为 5%。此外,一些模型预测的不是绝对风险而是治疗益处,即“预计患者 X 的风险绝对降低 2%”而不是“患者 X 有 20% 的事件绝对风险”,此类模型可使用决策曲线分析的替代版本。
曲线需要达到多少差异?
在经典决策理论中,应选择具有最高预期效用的策略,而不管收益的大小或统计显着性如何。因此,从理论上讲,净收益的任何改善都是值得的。也就是说,直接的决策分析没有考虑获取数据和实施模型的真实情况,比如时间、成本等。现在,如果一个模型需在净收益方面只有很小的改进,我们可能不会使用该模型。这个问题有两种方法。首先,如关于06年净收益的原始论文中提到,研究人员可以将与模型或测试相关的危害纳入决策曲线。简而言之,研究人员会问:“如果测试/模型是完美的,我会接受从多少患者中才能找到一个真实的病例(例如癌症)?”。这个数字的倒数被称为“测试伤害test harm”,并从净收益中减去。或者,研究人员可以查看净收益的差异或被避免的干预,并做出非正式的判断;这与“测试权衡test trade-off”的概念有关。使用图 3 中显示的数据,有人可能会问是否值得为 100 名患者去避免39次活检,或者是否值得使用模型而不是测试来避免5次活检。这些问题的答案取决于模型和测试所需的信息类型,例如是否需要侵入性、有害性或成本。
决策曲线是否应该有置信区间或p值?
统计显着性和置信区间不是经典决策理论中的重要概念。决策者应该首先考虑给定决策问题的所有合理选择。哪些选项算作“合理”可能涉及对统计显着性的考虑。但是在不同选项之间进行选择时,最理性的选择(通常)是具有最高预期效用的选择,而与统计显着性无关。作为一个简单的实验,假设一个人必须赶回家去赴约,可以选择两条公交路线中的任何一条,并且碰巧拥有每条路线的时间数据集。如果回家的平均时间是30和35分钟,分布和方差相似,则建议个人采取更快的回家路线,即使差异在统计上不显着并且时间差异的置信区间与零重叠。因此,很少有已发布的决策曲线包含置信区间。置信区间在某些情况下可能很有用,例如,确定是否需要进行更多研究。DCA分析也有了计算置信区间的方法。
曲线下面积 (AUC) 优于 0.50,模型是否会是有害的?
如果一种模型的 AUC 比另一种更好,那么它的净收益怎么会更差呢?净收益同时考虑了判别 (AUC) 和校准。举一个简单的例子,假设我们将前列腺癌的预测除以 10。尽管这对 AUC 没有影响——风险较高的患者比风险较低的患者更有可能患高级别癌症——它会对临床应用产生明显的影响:我们可能会告诉一个风险为 40% 的患者,风险仅为 4%。有了这个风险估计,他会选择不进行活检,从而有漏诊侵袭性癌症的风险。
为什么“干预所有人intervention for all”或者 “不干预任何人intervention for none”只是一个相对比较 ?
在许多情况下,无论测试或模型结果如何,对所有患者进行干预或者不干预都是合理的临床策略。 必须找到优于这两种策略的测试或模型,以证明在临床实践中使用是合理的。有文献中证明了将模型与干预或者不干预进行比较的价值。 例如Nam等人发现在高风险时,前列腺活检模型的净收益低于对所有高风险男性进行活检,原因该模型低估了患癌症的风险。
决策曲线分析能否替代传统的决策分析或成本效益分析?
决策曲线分析比完整的决策分析更快、更容易,因为它需要指定的参数更少(实际上,只有一个,阈值概率的合理范围)。但是,这样做的前提是简化假设。如果决策曲线分析的结果非常清楚,例如,模型没有任何好处,则可能不需要进行更复杂的决策分析。另一方面,如果结果模棱两可,则可能需要进行决策分析,其中包含更完整的收益、危害和成本参数列表。
可以使用决策曲线来选择最佳阈值吗?
这是一个常见且基本的误解。研究人员有时会写出诸如“模型在30–40%范围内效果比较好;或者写到如果模型预测的概率大于 30 – 40%,患者则应选择干预。”这颠倒了阈值概率和模型评估之间的关系。研究人员应首先在考虑避免干预对患病患者与不必要干预对无病患者的相对危害的基础上,计算出临床上合理的阈值概率范围。然后,再确定他们的模型或测试的净收益是否优于这个阈值概率范围内的替代方案。
如何在临床中使用决策曲线分析?
与新药试验的 p 值和总体绝对风险降低值相比,决策曲线分析没有直接的临床适用性。在药物试验中,可能会使用一个 p 值来得出“药物有效”和总体绝对风险降低的结论,以判断“药物的益处大于危害”。在这种情况下,医生会在需要时将药物给予患者,而无需每次都查看试验结果。以类似的方式,决策曲线用于评估模型或测试是否对临床有益。如果结果是肯定的,那么模型或测试可以与患者疾病情况一起使用,作为共同决策的一部分,而无需重新参考原始决策曲线。
在我使用决策曲线的结果和使用测试或模型的结果之前,我是否需要知道个别患者的阈值概率?
这不是决策曲线的用途。 如果一个模型或测试在整个合理阈值概率范围内具有最高的净收益,那么无论患者偏好如何,都应该使用该模型或测试。如果最佳方法取决于阈值概率,那么典型的结论将是模型或测试具有未经证实的益处,或者它仅在我们假设的特定范围中有用。更正式的决策分析可能涉及从研究样本中引出个人偏好和在这些偏好的分布中整合效用(utilities)。
结论
截至2017 年,PubMed 搜索“决策分析”检索到311篇论文;对“决策曲线分析”搜索检索到95篇。鉴于如果没有直接有效的分析技术,只有较少的决策曲线论文会涉及决策分析方法,这意味着在医学文献中,决策分析需要加大引入决策曲线分析。因此,对决策曲线分析的更深入理解不仅具有内在价值,而且还将帮助整个研究界加深对决策分析原则的理解。
当研究人员向我们指出“决策曲线分析很难理解”时,这明显是对度量(metric)产生了混淆,而非方法。决策曲线的计算只需要最简单的数学,但阈值概率和净收益这两个指标对许多人来说都是新概念。
这篇文章希望有助于解读决策曲线分析,并支持决策曲线的基本概念得到更广泛的理解。
参考
2006年Vickers AJ, Elkin EB提出来的DCA分析Decision curve analysis: a novel method for evaluating prediction models. Med Decis Making
本文主要翻译A simple, step-by-step guide to interpreting decision curve analysis
现成代码 https://www.mskcc.org/departments/epidemiology-biostatistics/biostatistics/decision-curve-analysis
其他文章介绍具体步骤和代码https://atm.amegroups.com/article/view/20389/pdf
还有其他的R包https://www.danieldsjoberg.com/dcurves/articles/dca.html,https://cran.r-project.org/web/packages/ggDCA/index.html
#####################################################################
#版权所有 转载请告知 版权归作者所有 如有侵权 一经发现 必将追究其法律责任
#Author: Jason
#####################################################################
文章作者 zzx
上次更新 2022-04-30
