总结连锁不平衡的一些知识，内容来源(copy)网络。

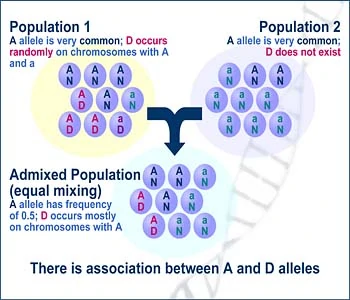
1、LD的概念

连锁不平衡（linkage disequilibrium, LD）分析是群体遗传学研究中常见的分析内容，当位于某一座位的特定等位基因与另一座位的某一等位基因同时出现的概率大于群体中因随机分布的两个等位基因同时出现的概率时，称这两个座位处于连锁不平衡状态。

连锁不平衡性是指在两个或者多个位点上的非随机关联性，这些位点既可能在同一条染色体上，也可以在不同的染色体上。连锁不平衡性也被称作配子水平的不平衡性或配子不平衡性。从另一个角度讲，连锁不平衡是等位基因或者遗传标记在一个人群中表现出高于或低于由等位基因的随机频率而预测的单模标本的频率。连锁是指染色体上的两个或者多个位点进行有限的组合，而连锁不平衡性不等同于连锁。连锁不平衡的数量取决于观察和预期的位点频率的差异。对于那些重组后位点或者基因型的频率等于预期的群体我们称其为连锁平衡。连锁不平衡的程度取决于多方面的因素，包括遗传连锁，选择，和重组的概率，遗传漂变，选型交配以及群体结构，都会影响LD的变化。

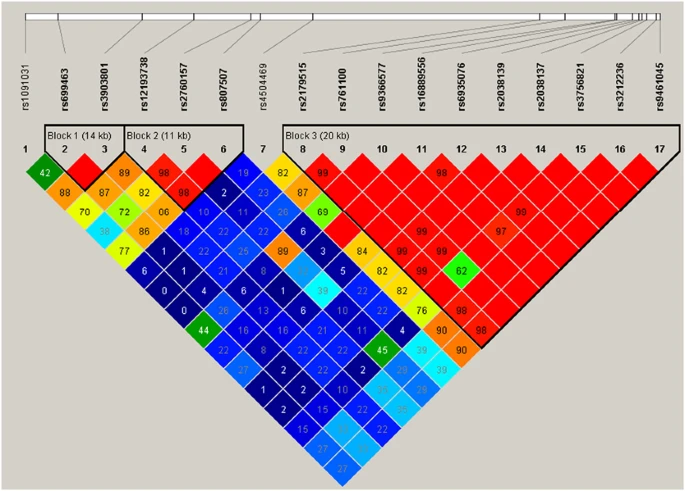
上图展示了由Haploview软件生成的连锁不平衡块Linkage disequilibrium (LD) block，LD用 D′ statistic衡量，颜色从蓝到红表示LD的高低（https://doi.org/10.1038/jhg.2016.40）。

2、LD的计算方法与度量指标

	B	b
A	AB观察值P(AB)	Ab观察值P(Ab)	A的频率P(A)
a	aB观察值P(aB)	ab观察值P(ab)	a的频率P(a)
	B的频率P(B)	b的频率P(b)	1

主要基于观察到的单倍型的频率与期望单倍型频率之间的差异。比如通过a和b的频率，我们可以计算期望出现的频率为P(A)*P(B)，而真实观察到的是P(AB)。至于这些差异，我们一帮用D，D’和r2来表示LD的程度。

衡量指标	公式	优势	缺点
D	D=P(AB)-P(A)*P(B)	容易理解	受等位基因的频率影响很大
D'	D' = D/Dmax	对评估历史重组概率（historical recombination probability）有用	依赖样本量，受低频等位基因影响大，此时D’被高估
r²	r²= D²/P(A)P(a)P(B)P(b)	可以用于关联分析研究中的样本量评估，tagSNP的筛选	受等位基因的频率和样本量影响

D值 - D statistic的计算

1

D=P(AB)-P(A)*P(B)

如果D值显著偏离0，则说明存在LD。如果接近0，则说明两个位点趋于连锁完全平衡，随机组合。

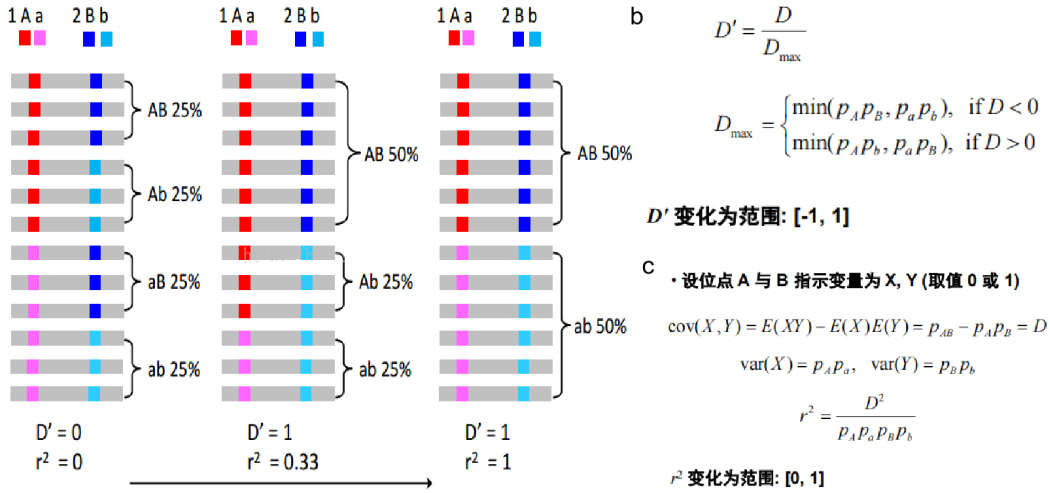
标准化指标：D'（Standardized D）

由于D值严格依赖于等位基因频率（allele frequency），故不适合应用于表述实际的LD强度。标准化的不平衡系数D’能够避免这种对等位基因频率的依赖。D’的取值范围为-1到1。

1
2
3
4
5


D'=D/Dmax
当D<0, Dmax=min{P(A)P(B),P(a)P(b)}；
当D>0, Dmax=min{P(A)P(b),P(a)P(B)}；
当D'=1，表示连锁完全不平衡，没有重组；
当D'=0，表示连锁完全平衡，随机组合

但D’也有它的局限性

比如当单倍型为2种或3种时，|D'|一定等于1，但是当|D'|<1时，D’的值究竟表示多大程度的连锁不平衡，是很难做出准确判断的。
另外D’严格依赖于样品的大小。如果样本偏少时，snp数量比较少，这样算出来的D’就会偏大，尤其是某个位点其中一个等位基因频率很低时，因此较高D’背后，实际上可能是连锁不平衡程度很低的两个位点。
统计学上较高的D’值同源重组发生率低，而普通程度的D'<1不适合度量LD，以及比较不同研究之间的LD程度，因此只有统计学上显著性接近1的D’值才能够解释这两个位点之间的重组历史，而D’则不能用来研究这种情况。
D’对基因频率的变化不敏感，当其中一个位点的一个基因频率比较低的时候，r2比 D’要更可靠一些。

标准化指标：r²

这时就需要引进r2来表示LD，r=pearson coefficient of correlation，r2的计算方法如下：

1
2
3


r2=D*D/(P(A)P(a)P(B)P(b))
当r2=1，表示连锁完全不平衡，没有重组，提示两位点将产生完全相同的信息（所以,选择tagSNP时会参考r2）
当r2=0，表示连锁完全平衡，随机组合

r2的取值范围为0到1，反映两个位点之间的“correlation coefficient”。R2=1有更严格的解释：两个位点的等位基因有相同的频率，并且一个位点某个等位基因的出现完全预示着另外一个位点相应等位基因的出现，这时候两个位点组成的四种可能的单倍型仅表现为两种。与D’相比，r2在连锁不平衡中更加有用，因为其具有较强的群体遗传学理论基础和一些统计学上的优势：

r2的期望值和有效种群大小和重组系数相关，r2=1/(1+4NeC),其中Ne是有小种群大小，C是重组系数。
r2有很好的取样特性，样本量和r2的乘积就是所观察到的关联水平概率对应的卡方值。在检测snp和致病位点之间的关联时，如果要达到同样的统计效力，所需要的样本量要增大1/r2倍。例如，假设snp1与疾病相关，我们要对它附近的snp2进行基因分型，他们之间的LD系数r2=0.5，为了达到与snp1位点检测相同的统计效力，必须把样本增加2倍。
与D’相比，在同样长度的染色体范围内，r2往往更低，这个特性能够帮助我们找到更精度的基因定位。
另外，r2和D’相比，受样本量和等位基因频率的影响较小（但影响仍然存在）。

D’和r²不一致时

D’和r2是不同的归一化D的方法，在其他方法中也很流行。D' 使用 D 的理论最大值进行归一化，r-squared 使用相关系数。

D' 和 r2 有很大的不同，因为 D' 的高值并不意味着一个基因座可以高精度地预测另一个基因座，这在填充SNP（imputating SNP）的情况下可能是一个主要问题。另一方面，r2 为 1 意味着完美的可预测性；如果我们知道一个基因座的等位基因，我们可以完美地预测第二个基因座的等位基因，反之亦然。

计算举例

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


# 1 
P(A)=0.5, P(a)=0.5, P(B)=0.5, P(b)=0.5
D=0.25-0.5*0.5=0
D'=r2=0

# 2  
P(A)=0.75, P(a)=0.25, P(B)=0.5, P(b)=0.5
D=0.5-0.75*0.25=0.125
D'=0.125/min{0.75*0.5, 0.25*0.5}=1
r2=0.125*0.125/(0.75*0.25*0.5*0.5)=0.33

# 3 
P(A)=0.5, P(a)=0.5, P(B)=0.5, P(b)=0.5
D=0.5-0.5*0.5=0.25
D'=0.25/min{0.5*0.5, 0.5*0.5}=1
r2=0.25*0.25/(0.5*0.5*0.5*0.5)=1

LD block

一段区域内95%以上的SNP间D’值的95%CI在(0.7-0.98)之间，在说明该区域几乎没有发生重组。(Gabriel SB, 2002, The structure of haplotype blocks in the human genome)

LD衰减decay

一般而言，两个位点在基因组上离得越近，相关性就越强，LD系数就越大。反之，LD系数越小。也就是说，随着位点间的距离不断增加，LD系数通常情况下会慢慢下降。这个规律，通常就会使用LD衰减图来呈现。

LD衰减指位点间由连锁不平衡到连锁平衡的演变过程；LD衰减的速度在不同物种间或同物种的不同亚群间，差异非常大。所以，通常会使用“LD衰减距离”来描述LD衰减速度的快慢，不同文章中“LD衰减距离”标准不同，常见的标准有：LD系数降低到最大值的一半、LD系数降低到0.5以下、LD系数降低到不同物种的基线水平等。

LD衰减距离在群体遗传学中的应用也非常广泛，一方面可以判断GWAS所需标记量，决定GWAS的检测效力以及精度；另外也可以辅助分析进化与选择，在同一个连锁群上，LD衰减慢说明该群体受到选择，一般来说，野生群体比驯化改良群体LD衰减快，异花授粉植物比自花授粉植物LD衰减快。

这是因为在一段 DNA 序列中，位点与位点之间存在着连锁的关系。不同位点间的连锁构成了“单倍体型”，随着重组的积累，特定的单倍体型会被削弱而逐渐消失。由于重组率与连锁距离有关，所以连锁不平衡范围会逐渐缩短，如下面的图所示，40代的小鼠的LD block长度和LD的值都很低。对于新产生的一个单倍体型，由于重组来不及破坏位点之间的连锁，所以它们之间连锁不平衡的距离往往比较远。在中性条件下，如果某个单倍体型是较新产生的，那么它的频率往往较低，而频率较高的单倍体型，需要经历很长一段时间才可能因为受到随机漂变的影响达到较高的频率。如果群体经历了正向选择，那么与有利位点连锁的周围位点会由于搭载效应而导致频率很快提升，所以包含有利位点的单倍体型一方面有着较高的频率，另一方面由于经历的时间不长，因此也有这较长的 LD 影响范围。这种特征为检测是否发生了正向选择提供了一个有效的突破点。

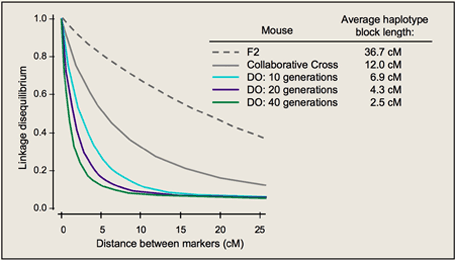
一般而言，LD系数大于0.8就是强相关。如果LD系数小于0.1，则可以认为没有相关性。如果LD衰减到0.1这么大的区间内都没有标记覆盖的话，即使这个区间有一个效应很强的功能突变，也是检测不到关联信号的。所以，通常可以通过比较LD衰减（到0.1）距离和标记间的平均距离，来判断标记是否对全基因组有足够的覆盖度。(GWAS标记量=基因组大小/LD衰减距离)。

对于LD衰减速率慢的物种来说，距离比较远的标记也可以与目标基因紧密连锁，用于标记辅助选择，但是同时也比较难打破目标基因与其他负效应基因的连锁。另外进化过程中与驯化相关的基因受到选择，由于邻近效应，其侧翼的序列也受到选择，最终使得这个区域LD值变大。这个也被用于作为进化分析中筛选selective sweep区间的候选参数。

常用的计算 LD 的软件为 PLINK ，但不支持直接读取 VCF 格式的文件，使用 PLINK 计算 LD 之前需要先将 VCF 格式的文件转换为 PED 格式或 bed + bim + fam 的格式。这样的格式转换会造成额外的存储负担。而另一款软件PopLDdecay 一个主要的优点在于可以读取 VCF 格式的文件，直接生成 LD 统计数据并画出 LD 的衰减图。PopLDdecay的输入文件是VCF文件（变异检测的结果文件），可由开源软件GATK产生。通过“-MAF”、“-Miss”和“-Het”参数根据MAF值、缺失率和杂合率过滤SNP。最后会输出D’ 、r2值和LD decay图。如果输入文件是phased VCF文件，那么PopLDdecay软件包还可以用于计算EHH值，这个参数在群体选择分析研究中有时也会用到。

根据LOD、r2 对在Block选择tagSNP

LOD(log odds score method): 遗传连锁的一种计算，定义为连锁基因的可能性数据与非连锁基因的可能性数据之比率的log10。通常判定连锁关系是以Lod值大小为依据。
Lod值为0，意味着连锁假设与不连锁假设的可能性相等；Lod值为正值，有利于连锁；Lod值为负值，表示有一定重组率的连锁。
显著的域值是＋3和－2。当Lod>+1时,表示存在连锁; Lod>+3时(即odd=1000:1),表示肯定连锁, 连锁的概率为95%; Lod<-2时,表示否定连锁.
通过LD数据比对，挑选出每个block中r2>0.8，且LOD>3的SNPs，选取平均值最大的一个SNP作为该单倍域标签SNP。有时在同一个单倍域中，SNPs连锁不平衡程度低，不能相互替代，因此全选出作为tagSNP

linkage和association都是定位性状loci的策略

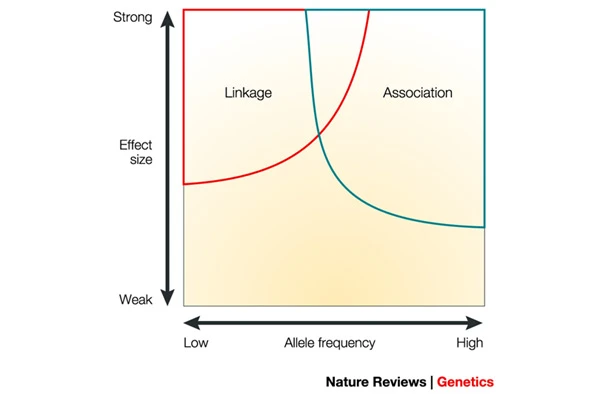
连锁不平衡研究和关联研究往往有相似的地方，1986年Lander和Botstein提出了基于LD来筛选人类基因组中与疾病有关的loci，1994年Houwen则提供了可以筛选的证据。关联分析也是检验群体中疾病或者性状和等位基因间是否存在相关性，2005年第一例GWAS研究出现，利用了116,204个SNPs的信息。在复杂疾病的分析中，关联分析比连锁分析更为优越。通常，当易感变异频繁出现时，关联研究比连锁研究更有效。尽管对“构成常见疾病的常见变异”有一定的支持，但仍有很多争论和很少的经验例子来解决它（这也是大家对GWAS的质疑）。在任何特定研究中，可检测效应大小的精确大小将主要取决于样本大小。随着样本量的增加，可以识别出影响越来越小的等位基因。请注意，对于弱作用的等位基因，目前所有的方法都是不充分的。

关联分析也是随着SNP分型技术比如SNP芯片的发展而产生，现在很容易实现大规模的SNP分型（1000到10000人的疾病病例和对照研究）。