特征选择是机器学习中的一个重要步骤,通过特征选择挑选出对预测起重要作用的变量,既可以减少数据的维度,也可以减少计算的消耗,同时也有助于我们对自己的数据的理解。有许多方法都可以应用到特征选择,比如大家常用的LASSO。我在用R做数据分析的时候,看到过这个帖子,进而了解了很多算法,所以对这个帖子进行了翻译,方便自己复习,也方便大家学习。
原文参考: https://www.machinelearningplus.com/machine-learning/feature-selection/
- Boruta
- Variable Importance from Machine Learning Algorithms
- Lasso Regression
- Step wise Forward and Backward Selection
- Relative Importance from Linear Regression
- Recursive Feature Elimination (RFE)
- Genetic Algorithm
- Simulated Annealing
- Information Value and Weights of Evidence
- DALEX Package
Introduction
真实的数据中,有些变量可能仅是噪声,并没有多少重要意义。
这类变量占用内存空间、消耗计算资源,我们最好去除这类变量,特别是在很大的数据集中。
有时候,我们有一个具有业务意义的变量,但不确定它是否确实有助于预测Y。还有一个事实:在一个机器学习算法中有用的特征(例如决策树) 可能其他算法中(例如回归模型)不被选用或者低估。
同时,有些变量单独预测Y的性能不好,但与其他预测变量/特征组合的情况下却非常显著。比如说有些变量与预测指标的相关性很低,但在其他变量参与的情况下,它可以帮助解释某些其他变量无法解释的模式/现象。
在这些情况下,很难决定包含还是去掉这些变量/特征。
这里讨论的策略可以解决这些问题,同时可以帮助理解对于一个模型而言,变量的重要性与否importance,以及对模型有多少贡献。
重要的一点是,我们最希望使用的变量是既具有业务意义同时也有重要性方面的指标。
我们这里导入Glaucoma 数据集,此数据集的目标是通过63个不同的生理测量指标来预测青光眼的与否。
1
2
3
4
5
6
|
# Load Packages and prepare dataset
library(TH.data)
library(caret)
data("GlaucomaM", package = "TH.data")
trainData <- GlaucomaM
head(trainData)
|
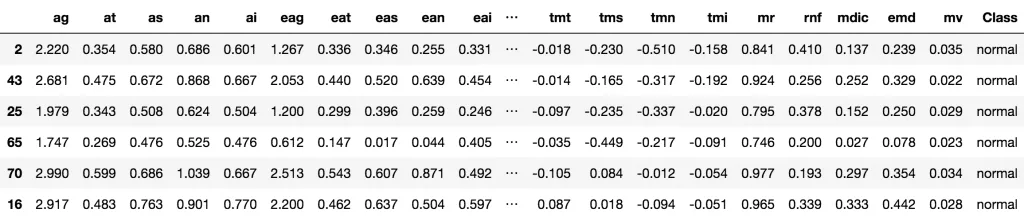
Glaucoma数据集
1. Boruta
Boruta 是一个基于随机森林对特征进行排名和筛选的算法。
Boruta 的优势是它可以明确的决定变量是否重要,并且帮助选择那些统计显著的变量。此外,可以通过调整p值和maxRuns来调整算法的严格性。
maxRuns是算法运行的次数,该参数值越大,会选择出更多的变量。默认是100.
在决定特征是否重要的过程中,一些特征可能会被标为Tentative。有时增加maxRuns或许可以解决特征的暂定行Tentativeness。
以TH.data的Glaucoma数据集为例子。
1
2
|
# install.packages('Boruta')
library(Boruta)
|
Boruta的方程用的公式同其他预测模型类似,响应变量response在左边,预测变量在右边。
如果预测变量处输入的是点,则意味着所有变量都会纳入评价中。
doTrace参数控制打印到终端的数目。该值越高,打印的log信息越多。为了节省空间,这里设置0,你可以设置1和2试试。
结果输出在boruta_output.
1
2
|
# Perform Boruta search
boruta_output <- Boruta(Class ~ ., data=na.omit(trainData), doTrace=0)
|
看看里面包含哪些内容
1
2
3
4
5
6
7
8
9
10
11
|
names(boruta_output)
1. ‘finalDecision’
2. ‘ImpHistory’
3. ‘pValue’
4. ‘maxRuns’
5. ‘light’
6. ‘mcAdj’
7. ‘timeTaken’
8. ‘roughfixed’
9. ‘call’
10. ‘impSource’
|
1
2
3
4
5
6
7
|
# 得到显著的或者潜在的变量
boruta_signif <- getSelectedAttributes(boruta_output, withTentative = TRUE)
print(boruta_signif)
[1] "as" "ean" "abrg" "abrs" "abrn" "abri" "hic" "mhcg" "mhcn" "mhci"
[11] "phcg" "phcn" "phci" "hvc" "vbss" "vbsn" "vbsi" "vasg" "vass" "vasi"
[21] "vbrg" "vbrs" "vbrn" "vbri" "varg" "vart" "vars" "varn" "vari" "mdn"
[31] "tmg" "tmt" "tms" "tmn" "tmi" "rnf" "mdic" "emd"
|
如果不确定潜在的变量是否保留,可以对boruta_output进行TentativeRoughFix
1
2
3
4
5
6
7
|
# Do a tentative rough fix
roughFixMod <- TentativeRoughFix(boruta_output)
boruta_signif <- getSelectedAttributes(roughFixMod)
print(boruta_signif)
[1] "abrg" "abrs" "abrn" "abri" "hic" "mhcg" "mhcn" "mhci" "phcg" "phcn"
[11] "phci" "hvc" "vbsn" "vbsi" "vasg" "vbrg" "vbrs" "vbrn" "vbri" "varg"
[21] "vart" "vars" "varn" "vari" "tmg" "tms" "tmi" "rnf" "mdic" "emd"
|
这样Boruta就代表我们来决定是否保留Tentative变量。查看这些变量的重要性分值。
1
2
3
4
|
# Variable Importance Scores
imps <- attStats(roughFixMod)
imps2 = imps[imps$decision != 'Rejected', c('meanImp', 'decision')]
head(imps2[order(-imps2$meanImp), ]) # descending sort
|
|
meanImp |
decision |
| varg |
10.279747 |
Confirmed |
| vari |
10.245936 |
Confirmed |
| tmi |
9.067300 |
Confirmed |
| vars |
8.690654 |
Confirmed |
| hic |
8.324252 |
Confirmed |
| varn |
7.327045 |
Confirmed |
用画图的形式来展示变量的重要性
1
2
|
# Plot variable importance
plot(boruta_output, cex.axis=.7, las=2, xlab="", main="Variable Importance")
|
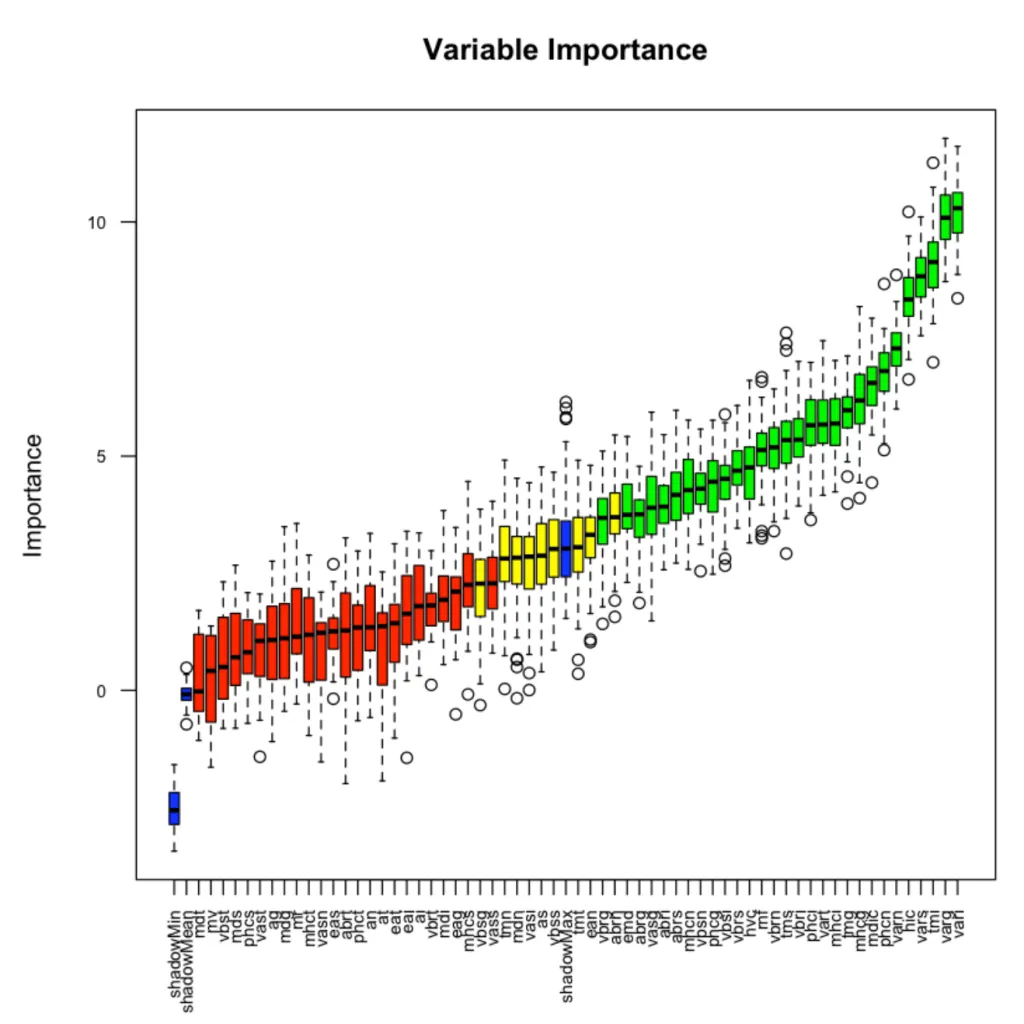 Variable Importance Boruta
Variable Importance Boruta
这幅图展示了每个变量的重要性。
绿色表示的是筛选出的变量confirmed,红色则是需要提出的变量,蓝色不是真实的特征,待变的是ShadowMax 和 ShadowMin,用来决定变量重要性与否。
2. Variable Importance from Machine Learning Algorithms
另外一种特征选择的方法是将各种ML算法最常用的变量视为最重要的变量。
根据机器学习算法学习X与Y之间关系的方式,不同的机器学习算法选出不同的变量(大多数是重叠的),但赋予的权重并不相同。
例如,在基于树的算法(如“ rpart”)中被证明有用的变量在基于回归的模型中可能没那么有用。 因此,不同算法没必要用相同的变量。
那么对于一个特定的机器学算法,如何找到变量的重要性?
-
利用caret 包中的train()一个特定的模型
-
使用 varImp() 来决定变量的重要性。
可能尝试多种算法,以了解各种算法之间的重要变量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
# 训练rpart模型,计算变量重要性
library(caret)
set.seed(100)
rPartMod <- train(Class ~ ., data=trainData, method="rpart")
rpartImp <- varImp(rPartMod)
print(rpartImp)
rpart variable importance
only 20 most important variables shown (out of 62)
Overall
varg 100.00
vari 93.19
vars 85.20
varn 76.86
tmi 72.31
vbss 0.00
eai 0.00
tmg 0.00
tmt 0.00
vbst 0.00
vasg 0.00
at 0.00
abrg 0.00
vbsg 0.00
eag 0.00
phcs 0.00
abrs 0.00
mdic 0.00
abrt 0.00
ean 0.00
|
rpart仅使用了63个功能中的5个,如果仔细观察,这5个变量位于boruta选择的前6个中。
让我们再做一件事:正则随机森林(Regularized Random Forest ,RRF)算法中的变量重要性。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
# Train an RRF model and compute variable importance.
set.seed(100)
rrfMod <- train(Class ~ ., data=trainData, method="RRF")
rrfImp <- varImp(rrfMod, scale=F)
rrfImp
RRF variable importance
only 20 most important variables shown (out of 62)
Overall
varg 24.0013
vari 18.5349
vars 6.0483
tmi 3.8699
hic 3.3926
mhci 3.1856
mhcg 3.0383
mv 2.1570
hvc 2.1357
phci 1.8830
vasg 1.8570
tms 1.5705
phcn 1.4475
phct 1.4473
vass 1.3097
tmt 1.2485
phcg 1.1992
mdn 1.1737
tmg 1.0988
abrs 0.9537
plot(rrfImp, top = 20, main='Variable Importance')
|
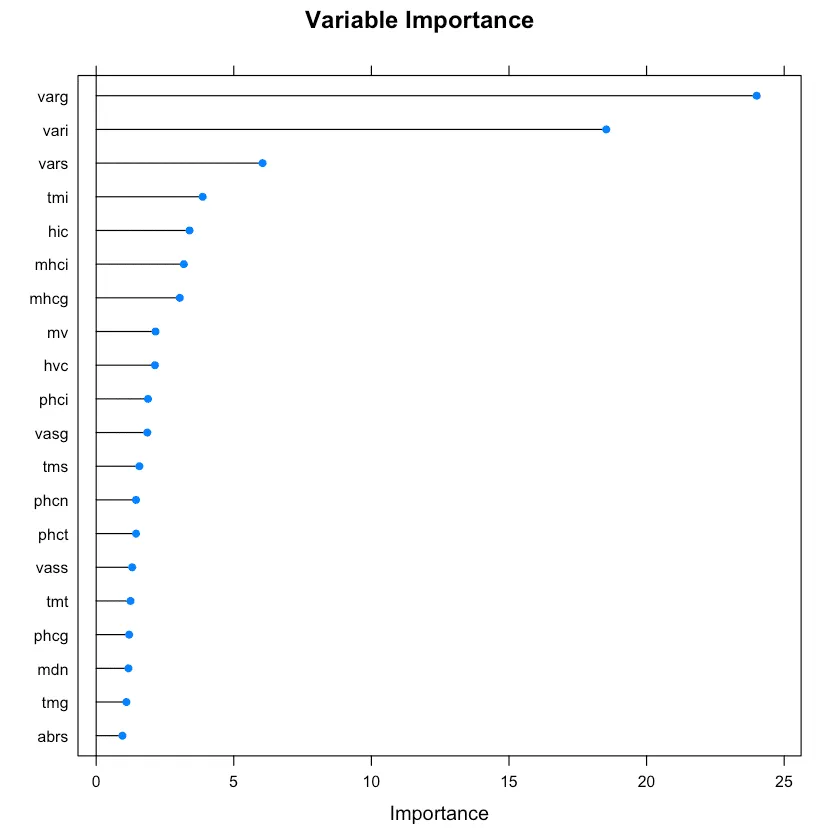 正则随机森林中的变量重要性。
正则随机森林中的变量重要性。
最前面的重要变量也于Boruta选择的吻合
其它的在train()中可以用的算法也可以用varImp计算变量的重要性:包括
ada, AdaBag, AdaBoost.M1, adaboost, bagEarth, bagEarthGCV, bagFDA, bagFDAGCV, bartMachine, blasso, BstLm, bstSm, C5.0, C5.0Cost, C5.0Rules, C5.0Tree, cforest, chaid, ctree, ctree2, cubist, deepboost, earth, enet, evtree, extraTrees, fda, gamboost, gbm_h2o, gbm, gcvEarth, glmnet_h2o, glmnet, glmStepAIC, J48, JRip, lars, lars2, lasso, LMT, LogitBoost, M5, M5Rules, msaenet, nodeHarvest, OneR, ordinalNet, ORFlog, ORFpls, ORFridge, ORFsvm, pam, parRF, PART, penalized, PenalizedLDA, qrf, ranger, Rborist, relaxo, rf, rFerns, rfRules, rotationForest, rotationForestCp, rpart, rpart1SE, rpart2, rpartCost, rpartScore, rqlasso, rqnc, RRF, RRFglobal, sdwd, smda, sparseLDA, spikeslab, wsrf, xgbLinear, xgbTree.
3. Lasso Regression
最小绝对收缩和选择算子(LASSO,Least Absolute Shrinkage and Selection Operator)回归是一种用L1范数惩罚的正则化方法。
从根本上来说,要增加权重(系数值)会带来成本。 它被称为L1正则化,增加的成本,与权重系数的绝对值成正比。
结果,在收缩系数的过程中,最终将某些不需要的特征的系数全部减小到零。 也就是说,它删除了不重要的变量。
LASSO回归也可以被视为有效的变量选择技术。
1
2
3
4
5
6
7
8
9
10
11
12
|
library(glmnet)
trainData <- read.csv('https://raw.githubusercontent.com/selva86/datasets/master/GlaucomaM.csv')
x <- as.matrix(trainData[,-63]) # all X vars
y <- as.double(as.matrix(ifelse(trainData[, 63]=='normal', 0, 1))) # Only Class
# Fit the LASSO model (Lasso: Alpha = 1)
set.seed(100)
cv.lasso <- cv.glmnet(x, y, family='binomial', alpha=1, parallel=TRUE, standardize=TRUE, type.measure='auc')
# Results
plot(cv.lasso)
|
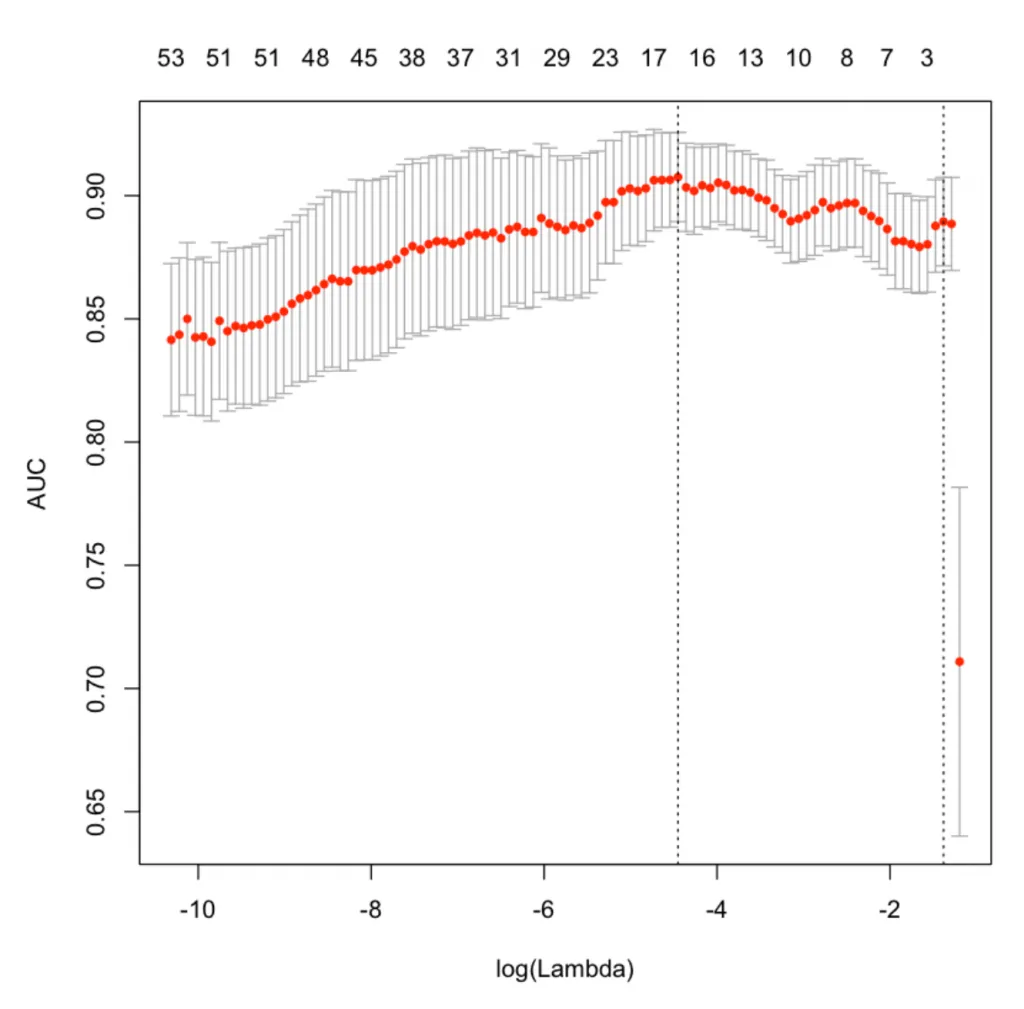
LASSO变量重要性
X轴是log之后的lambda,当是2的时候,lambda的真实值是100。
图的最上面显示了模型使用了多少个变量,相对应的红点Y值则是在这些变量使用的情况下,模型可以达到多少的AUC。
可以看到两条垂直虚线,左边的第一个指向具有最小均方误差的lambda。 右边的一个表示在1个标准偏差内偏差最大的变量的数量。
最优的lambda值存储在cv.lasso $ lambda.min中。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
|
# plot(cv.lasso$glmnet.fit, xvar="lambda", label=TRUE)
cat('Min Lambda: ', cv.lasso$lambda.min, '\n 1Sd Lambda: ', cv.lasso$lambda.1se)
df_coef <- round(as.matrix(coef(cv.lasso, s=cv.lasso$lambda.min)), 2)
# See all contributing variables
df_coef[df_coef[, 1] != 0, ]
Min Lambda: 0.01166507
1Sd Lambda: 0.2513163
Min Lambda: 0.01166507
1Sd Lambda: 0.2513163
(Intercept) 3.65
at -0.17
as -2.05
eat -0.53
mhci 6.22
phcs -0.83
phci 6.03
hvc -4.15
vass -23.72
vbrn -0.26
vars -25.86
mdt -2.34
mds 0.5
mdn 0.83
mdi 0.3
tmg 0.01
tms 3.02
tmi 2.65
mv 4.94
|
上面的输出显示了LASSO认为重要的变量。绝对值越高表示该变量越重要。
4. Step wise Forward and Backward Selection
如果Y变量是数字变量,则可以使用逐步回归来选择特征。 它特别用于选择最佳的线性回归模型。
它通过迭代地选择和删除变量,以找到具有尽可能低的AIC,来搜索最佳的回归模型。
可以使用step()函数来实现它,您需要为其提供基础的模型(该模型中的变量不再不去掉)和一个包含所有可能特征的模型。
这里的情况不是那么复杂(小于20个变量),我们可以在双向(forward和backward)上进行简单的逐步回归分析。
这里使用ozone数据集,其目的是根据天气有关的观测结果来预测ozone_reading。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
# Load data
trainData <- read.csv("http://rstatistics.net/wp-content/uploads/2015/09/ozone1.csv", stringsAsFactors=F)
print(head(trainData))
Month Day_of_month Day_of_week ozone_reading pressure_height Wind_speed
1 1 1 4 3 5480 8
2 1 2 5 3 5660 6
3 1 3 6 3 5710 4
4 1 4 7 5 5700 3
5 1 5 1 5 5760 3
6 1 6 2 6 5720 4
Humidity Temperature_Sandburg Temperature_ElMonte Inversion_base_height
1 20.00000 40.53473 39.77461 5000.000
2 40.96306 38.00000 46.74935 4108.904
3 28.00000 40.00000 49.49278 2693.000
4 37.00000 45.00000 52.29403 590.000
5 51.00000 54.00000 45.32000 1450.000
6 69.00000 35.00000 49.64000 1568.000
Pressure_gradient Inversion_temperature Visibility
1 -15 30.56000 200
2 -14 48.02557 300
3 -25 47.66000 250
4 -24 55.04000 100
5 25 57.02000 60
6 15 53.78000 60
|
读取数据之后,进行逐步回归。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
# Step 1: 定义基础的模型,只有截距
base.mod <- lm(ozone_reading ~ 1 , data=trainData)
# Step 2: 包含所有特征的模型
all.mod <- lm(ozone_reading ~ . , data= trainData)
# Step 3: 进行逐步回归算法,方向设置为双向forward and backward stepwise
stepMod <- step(base.mod, scope = list(lower = base.mod, upper = all.mod), direction = "both", trace = 0, steps = 1000)
# Step 4: 得到变量列表
shortlistedVars <- names(unlist(stepMod[[1]]))
shortlistedVars <- shortlistedVars[!shortlistedVars %in% "(Intercept)"] # remove intercept
# Show
print(shortlistedVars)
[1] "Temperature_Sandburg" "Humidity" "Temperature_ElMonte"
[4] "Month" "pressure_height" "Inversion_base_height"
|
所选模型具有上述6个变量。
但是,如果训练数据中的特征过多(> 100),最好将数据集拆分为10个变量的块,每个数据库中都必须包含Y。 遍历所有块并得到最优的变量。
这样做的原因是,有些变量在训练集特征很少的时候非常重要,但遇到线性模型有很多变量的时候,可能不会被选择出来。
最后,从入围的特征列表中,运行完整的逐步回归模型,以获取最终的选定特征集。
5. Relative Importance from Linear Regression
这个基数只针对线性回归模型。
相对重要性Relative importance可以用来评估哪些变量在解释线性模型的R平方值时起了多大作用。 因此,如果把重要性相加,那么它将总计为模型的R方值。
本质上,它不是直接选择特征的方法,因为模型中已经包含了特征。 但是,在建立模型之后,relaimpo可以计算每个变量对R方的贡献,或者换句话说,也就是在“解释Y变量”中的重要性。
那么,如何计算相对重要性呢?它在relaimpo软件包中实现。 通常,可以建立一个线性回归模型,并将其作为参数传递给calc.relimp()。relaimpo有多个选项可以计算相对重要性,但是推荐的方法是使用type =‘lmg’,如下所述。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
# install.packages('relaimpo')
library(relaimpo)
# Build linear regression model
model_formula = ozone_reading ~ Temperature_Sandburg + Humidity + Temperature_ElMonte + Month + pressure_height + Inversion_base_height
lmMod <- lm(model_formula, data=trainData)
# calculate relative importance
relImportance <- calc.relimp(lmMod, type = "lmg", rela = F)
# Sort
cat('Relative Importances: \n')
sort(round(relImportance$lmg, 3), decreasing=TRUE)
Relative Importances:
Temperature_ElMonte 0.214
Temperature_Sandburg 0.203
pressure_height 0.104
Inversion_base_height 0.096
Humidity 0.086
Month 0.012
|
此外,还可使用boostrapping(boot.relimp)来计算相对重要性的置信区间。
1
2
3
4
|
bootsub <- boot.relimp(ozone_reading ~ Temperature_Sandburg + Humidity + Temperature_ElMonte + Month + pressure_height + Inversion_base_height, data=trainData,
b = 1000, type = 'lmg', rank = TRUE, diff = TRUE)
plot(booteval.relimp(bootsub, level=.95))
|
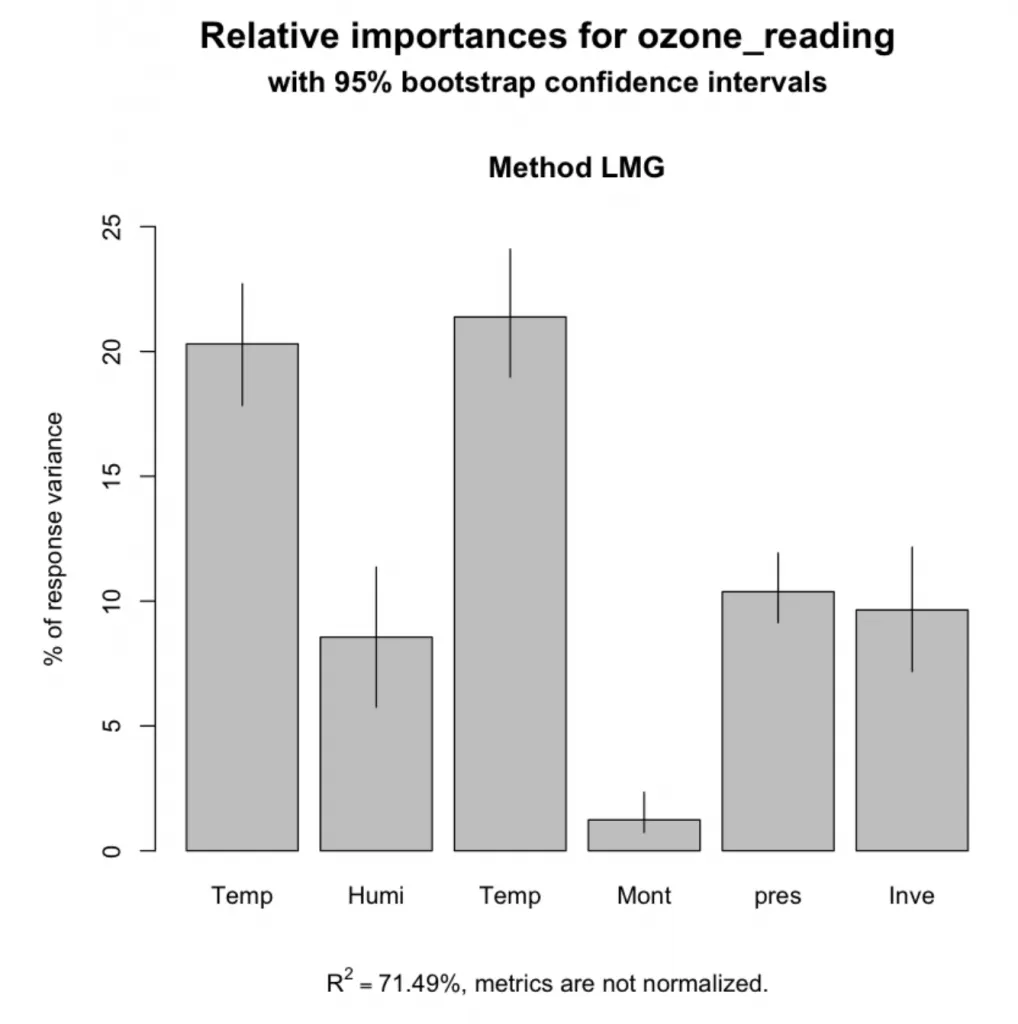 特征的相对重要性
特征的相对重要性
6. Recursive Feature Elimination (RFE)
递归特征消除Recursive feature elimnation (rfe)提供了一种严格的方法来确定重要变量,甚至可以将它们输入到机器学习算法中。
可以通过caret包的rfe()函数来使用,rfe()需要两个重要参数。
sizes决定了rfe应该迭代的最重要变量的数目(我们期望的重要变量数目)。 在下面,sizes设置为1到5、10、15和18。
其次,rfeControl参数接收rfeControl()的输出。 可以设置必须使用哪种机器学习算法来评估变量。 下面使用了基于rfFuncs的随机森林。 method =‘repeatedCV’意味着它将使用repeats = 5进行重复的k-fold交叉验证。
之后,可以得到每个size(前面设置的)的模型的accuracy和kappa值,最优的size的模型右边带有*标记。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
|
str(trainData)
'data.frame': 366 obs. of 13 variables:
$ Month : int 1 1 1 1 1 1 1 1 1 1 ...
$ Day_of_month : int 1 2 3 4 5 6 7 8 9 10 ...
$ Day_of_week : int 4 5 6 7 1 2 3 4 5 6 ...
$ ozone_reading : num 3 3 3 5 5 6 4 4 6 7 ...
$ pressure_height : num 5480 5660 5710 5700 5760 5720 5790 5790 5700 5700 ...
$ Wind_speed : int 8 6 4 3 3 4 6 3 3 3 ...
$ Humidity : num 20 41 28 37 51 ...
$ Temperature_Sandburg : num 40.5 38 40 45 54 ...
$ Temperature_ElMonte : num 39.8 46.7 49.5 52.3 45.3 ...
$ Inversion_base_height: num 5000 4109 2693 590 1450 ...
$ Pressure_gradient : num -15 -14 -25 -24 25 15 -33 -28 23 -2 ...
$ Inversion_temperature: num 30.6 48 47.7 55 57 ...
$ Visibility : int 200 300 250 100 60 60 100 250 120 120 ...
set.seed(100)
options(warn=-1)
subsets <- c(1:5, 10, 15, 18)
ctrl <- rfeControl(functions = rfFuncs,
method = "repeatedcv",
repeats = 5,
verbose = FALSE)
lmProfile <- rfe(x=trainData[, c(1:3, 5:13)], y=trainData$ozone_reading,
sizes = subsets,
rfeControl = ctrl)
lmProfile
Recursive feature selection
Outer resampling method: Cross-Validated (10 fold, repeated 5 times)
Resampling performance over subset size:
Variables RMSE Rsquared MAE RMSESD RsquaredSD MAESD Selected
1 5.222 0.5794 4.008 0.9757 0.15034 0.7879
2 3.971 0.7518 3.067 0.4614 0.07149 0.3276
3 3.944 0.7553 3.054 0.4675 0.06523 0.3708
4 3.924 0.7583 3.026 0.5132 0.06640 0.4163
5 3.880 0.7633 2.950 0.5525 0.07021 0.4334
10 3.751 0.7796 2.853 0.5550 0.06791 0.4457 *
12 3.767 0.7779 2.869 0.5511 0.06664 0.4424
The top 5 variables (out of 10):
Temperature_ElMonte, Pressure_gradient, Temperature_Sandburg, Inversion_temperature, Humidity
|
这里Temperature_ElMonte, Pressure_gradient, Temperature_Sandburg, Inversion_temperature, Humidity被选择为前五个重要变量(最优的model size是变量为10个的时候)
可以通过ref创建的lmProfile$optVariables来查看最终被选择出来的特征。
7. Genetic Algorithm
可以通过gafs()利用遗传算法进行有监督的特征选择。遗传算法消耗的计算资源较多,要小心设置gafsControl()中的迭代次数(iters)和repeats。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
|
# 定义control function
ga_ctrl <- gafsControl(functions = rfGA, # another option is `caretGA`.
method = "cv",
repeats = 3)
# 遗传算法特征选择
set.seed(100)
ga_obj <- gafs(x=trainData[, c(1:3, 5:13)],
y=trainData[, 4],
iters = 3, # normally much higher (100+)
gafsControl = ga_ctrl)
ga_obj
Genetic Algorithm Feature Selection
366 samples
12 predictors
Maximum generations: 3
Population per generation: 50
Crossover probability: 0.8
Mutation probability: 0.1
Elitism: 0
Internal performance values: RMSE, Rsquared
Subset selection driven to minimize internal RMSE
External performance values: RMSE, Rsquared, MAE
Best iteration chose by minimizing external RMSE
External resampling method: Cross-Validated (10 fold)
During resampling:
* the top 5 selected variables (out of a possible 12):
Month (100%), Pressure_gradient (100%), Temperature_ElMonte (100%), Visibility (90%), Inversion_temperature (80%)
* on average, 7.5 variables were selected (min = 5, max = 10)
In the final search using the entire training set:
* 6 features selected at iteration 3 including:
Month, Day_of_month, Wind_speed, Temperature_ElMonte, Pressure_gradient ...
* external performance at this iteration is
RMSE Rsquared MAE
3.6605 0.7901 2.8010
# Optimal variables
ga_obj$optVariables
1. ‘Month’
2. ‘Day_of_month’
3. ‘Wind_speed’
4. ‘Temperature_ElMonte’
5. ‘Pressure_gradient’
6. ‘Visibility’
|
上面列出了根据遗传算法得到的最佳变量。 但是暂时不会使用它,因为上述仅进行了3次迭代(为了节省计算时间),这是相当低的。
8. Simulated Annealing
模拟退火算法Simulated annealing是一个全局搜索算法,它允许接受次优解决方案,以期最终出现更好的解决方案。
它通过对初始解决方案进行随机的小改动,并查看性能是否得到了改善。 如果改动可以改善性能,则接受更改;不过,如果性能差异满足接受标准,则仍可以被接受。
在caret中,该算法已经在safs()中实现,接收使用safsControl()函数设置的控制参数。
safsControl类似于插入caret中的其他控制功能(例如rfe和ga中)。此外,它接受一个“ improve”参数,该参数是它需要等待而没有改进的迭代次数,直到将值重置为先前的迭代为止。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
|
# Define control function
sa_ctrl <- safsControl(functions = rfSA,
method = "repeatedcv",
repeats = 3,
improve = 5) # n iterations without improvement before a reset
# Genetic Algorithm feature selection
set.seed(100)
sa_obj <- safs(x=trainData[, c(1:3, 5:13)],
y=trainData[, 4],
safsControl = sa_ctrl)
sa_obj
Simulated Annealing Feature Selection
366 samples
12 predictors
Maximum search iterations: 10
Restart after 5 iterations without improvement (0.2 restarts on average)
Internal performance values: RMSE, Rsquared
Subset selection driven to minimize internal RMSE
External performance values: RMSE, Rsquared, MAE
Best iteration chose by minimizing external RMSE
External resampling method: Cross-Validated (10 fold, repeated 3 times)
During resampling:
* the top 5 selected variables (out of a possible 12):
Temperature_ElMonte (73.3%), Inversion_temperature (63.3%), Month (60%), Day_of_week (50%), Inversion_base_height (50%)
* on average, 6 variables were selected (min = 3, max = 8)
In the final search using the entire training set:
* 6 features selected at iteration 10 including:
Month, Day_of_month, Day_of_week, Wind_speed, Temperature_ElMonte ...
* external performance at this iteration is
RMSE Rsquared MAE
4.0574 0.7382 3.0727
# Optimal variables
print(sa_obj$optVariables)
[1] "Month" "Day_of_month" "Day_of_week"
[4] "Wind_speed" "Temperature_ElMonte" "Visibility"
|
在响应变量Y是二分类的时候,信息值Information Value可以用来判断预测变量(为分类变量)的重要性。这在逻辑回归和其他二分类的模型模型中表现的很好。
下面基于adult.csv数据集,来尝试找出哪些分类变量在预测个人是否赚取5万美元时起重要性。 运行下面的代码即可导入数据集。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
library(InformationValue)
inputData <- read.csv("http://rstatistics.net/wp-content/uploads/2015/09/adult.csv")
print(head(inputData))
AGE WORKCLASS FNLWGT EDUCATION EDUCATIONNUM MARITALSTATUS
1 39 State-gov 77516 Bachelors 13 Never-married
2 50 Self-emp-not-inc 83311 Bachelors 13 Married-civ-spouse
3 38 Private 215646 HS-grad 9 Divorced
4 53 Private 234721 11th 7 Married-civ-spouse
5 28 Private 338409 Bachelors 13 Married-civ-spouse
6 37 Private 284582 Masters 14 Married-civ-spouse
OCCUPATION RELATIONSHIP RACE SEX CAPITALGAIN CAPITALLOSS
1 Adm-clerical Not-in-family White Male 2174 0
2 Exec-managerial Husband White Male 0 0
3 Handlers-cleaners Not-in-family White Male 0 0
4 Handlers-cleaners Husband Black Male 0 0
5 Prof-specialty Wife Black Female 0 0
6 Exec-managerial Wife White Female 0 0
HOURSPERWEEK NATIVECOUNTRY ABOVE50K
1 40 United-States 0
2 13 United-States 0
3 40 United-States 0
4 40 United-States 0
5 40 Cuba 0
6 40 United-States 0
|
查看inputData中分类变量的信息值。
好了,现在让我们在inputData中找到分类变量的信息值。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
|
# 选择分类变量,用来计算信息值Info Value.
cat_vars <- c ("WORKCLASS", "EDUCATION", "MARITALSTATUS", "OCCUPATION", "RELATIONSHIP", "RACE", "SEX", "NATIVECOUNTRY") # get all categorical variables
# Init Output
df_iv <- data.frame(VARS=cat_vars, IV=numeric(length(cat_vars)), STRENGTH=character(length(cat_vars)), stringsAsFactors = F) # init output dataframe
# 得到每个变量的信息值
for (factor_var in factor_vars){
df_iv[df_iv$VARS == factor_var, "IV"] <- InformationValue::IV(X=inputData[, factor_var], Y=inputData$ABOVE50K)
df_iv[df_iv$VARS == factor_var, "STRENGTH"] <- attr(InformationValue::IV(X=inputData[, factor_var], Y=inputData$ABOVE50K), "howgood")
}
# Sort
df_iv <- df_iv[order(-df_iv$IV), ]
df_iv
|
|
VARS |
IV |
STRENGTH |
| 5 |
RELATIONSHIP |
1.53560810 |
Highly Predictive |
| 3 |
MARITALSTATUS |
1.33882907 |
Highly Predictive |
| 4 |
OCCUPATION |
0.77622839 |
Highly Predictive |
| 2 |
EDUCATION |
0.74105372 |
Highly Predictive |
| 7 |
SEX |
0.30328938 |
Highly Predictive |
| 1 |
WORKCLASS |
0.16338802 |
Highly Predictive |
| 8 |
NATIVECOUNTRY |
0.07939344 |
Somewhat Predictive |
| 6 |
RACE |
0.06929987 |
Somewhat Predictive |
信息值范围的含义
-
小于0.02,则预测变量对建模无用
-
0.02至0.1,则预测变量仅具有弱关系
-
0.1到0.3,则预测变量具有中等强度关系
-
0.3或更高,则预测变量具有很强的关系
这是关于信息值IV,那证据权重Weight of Evidence呢?证据权重可以帮助找出找出给定类别变量解释事件events(下表中的Goods)时的重要性。
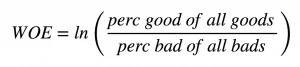 证据权重
证据权重
分类变量的信息值可以从对应的证据权重(WOE)中得到。
IV=(perc good of all goods - perc bad of all bads) * WOE
下面的WOETable列出了更详细的信息。
1
|
WOETable(X=inputData[, 'WORKCLASS'], Y=inputData$ABOVE50K)
|
| CAT |
GOODS |
BADS |
TOTAL |
PCT_G |
PCT_B |
WOE |
IV |
| ? |
191 |
1645 |
1836 |
0.0242940728 |
0.0665453074 |
-1.0076506 |
0.0425744832 |
| Federal-gov |
371 |
589 |
960 |
0.0471890104 |
0.0238268608 |
0.6833475 |
0.0159644662 |
| Local-gov |
617 |
1476 |
2093 |
0.0784787586 |
0.0597087379 |
0.2733496 |
0.0051307781 |
| Never-worked |
7 |
7 |
7 |
0.0008903587 |
0.0002831715 |
1.1455716 |
0.0006955764 |
| Private |
4963 |
17733 |
22696 |
0.6312643093 |
0.7173543689 |
-0.1278453 |
0.0110062102 |
| Self-emp-inc |
622 |
494 |
1116 |
0.0791147291 |
0.0199838188 |
1.3759762 |
0.0813627242 |
| Self-emp-not-inc |
724 |
1817 |
2541 |
0.0920885271 |
0.0735032362 |
0.2254209 |
0.0041895135 |
| State-gov |
353 |
945 |
1298 |
0.0448995167 |
0.0382281553 |
0.1608547 |
0.0010731201 |
| Without-pay |
14 |
14 |
14 |
0.0017807174 |
0.0005663430 |
1.1455716 |
0.0013911528 |
10. DALEX Package
DALEX是一个很强大的包,可以解释关于ML模型中使用的变量的各种事情。
例如,使用variable_dropout()函数,可以发现基于丢失损失的变量重要性,也就是说,从模型中删除变量会导致多少损失。
除此之外,它还具有single_variable()函数,当改变变量的值时,模型的输出将会如何改变。
它还可以通过 single_prediction()来拆分单个模型的预测值,从而了解哪个变量对Y值的预测产生了什么影响。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
|
library(randomForest)
library(DALEX)
# Load data
inputData <- read.csv("http://rstatistics.net/wp-content/uploads/2015/09/adult.csv")
# Train random forest model
rf_mod <- randomForest(factor(ABOVE50K) ~ ., data=inputData, ntree=100)
rf_mod
# Variable importance with DALEX
explained_rf <- explain(rf_mod, data=inputData, y=inputData$ABOVE50K)
# Get the variable importances
varimps = variable_dropout(explained_rf, type='raw')
print(varimps)
Call:
randomForest(formula = factor(ABOVE50K) ~ ., data = inputData, ntree = 100)
Type of random forest: classification
Number of trees: 100
No. of variables tried at each split: 3
OOB estimate of error rate: 17.4%
Confusion matrix:
0 1 class.error
0 24600 120 0.004854369
1 5547 2294 0.707435276
variable dropout_loss label
1 _full_model_ 852 randomForest
2 EDUCATIONNUM 842 randomForest
3 EDUCATION 843 randomForest
4 MARITALSTATUS 844 randomForest
5 FNLWGT 845 randomForest
6 OCCUPATION 847 randomForest
7 SEX 847 randomForest
8 CAPITALLOSS 847 randomForest
9 HOURSPERWEEK 847 randomForest
10 AGE 848 randomForest
11 RACE 848 randomForest
12 WORKCLASS 849 randomForest
13 RELATIONSHIP 850 randomForest
14 NATIVECOUNTRY 853 randomForest
15 ABOVE50K 853 randomForest
16 CAPITALGAIN 893 randomForest
17 _baseline_ 975 randomForest
plot(varimps)
|
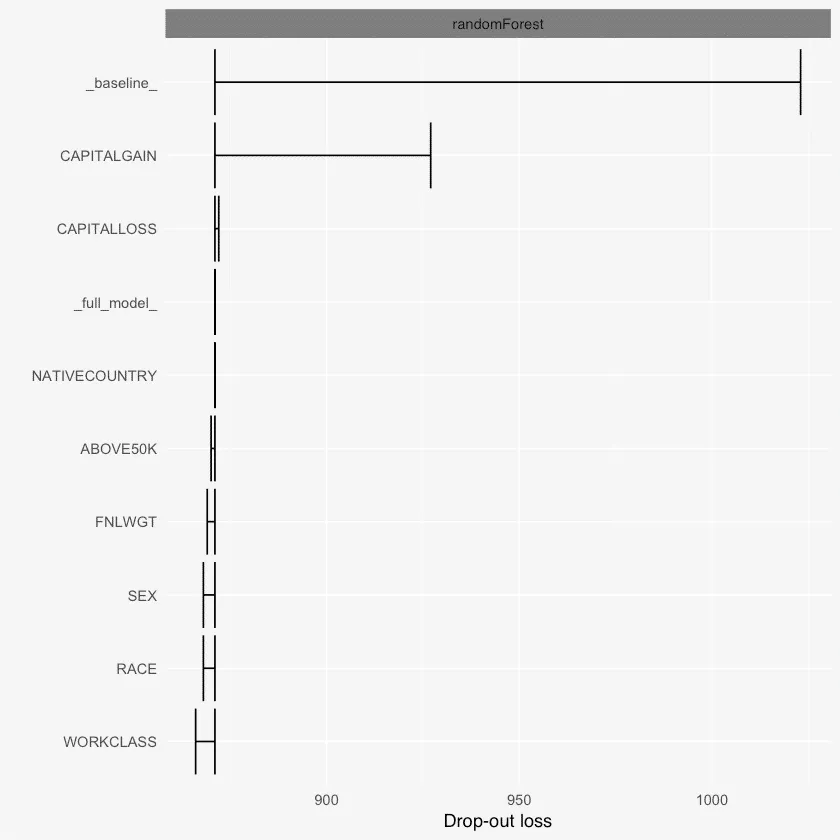 Dalex变量重要性
Dalex变量重要性
参考: https://www.machinelearningplus.com/machine-learning/feature-selection/

 Variable Importance Boruta
Variable Importance Boruta 正则随机森林中的变量重要性。
正则随机森林中的变量重要性。
 特征的相对重要性
特征的相对重要性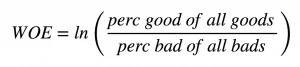 证据权重
证据权重 Dalex变量重要性
Dalex变量重要性